游戏中坐标空间的变换
蛮重要的知识,但是总有些地方会疏忽,特写此文来加强记忆,主要总结于《Shader入门精要》。
矩阵部分知识:
*正交矩阵:如果该矩阵与其转置矩阵乘积为单位矩阵则为正交矩阵,再进一步推导可得:$M^TM=MM^T=I$,$M^-M=I$,$M^-=M^T$
- 书中采用的都是列向量和矩阵进行相乘,这时式子的阅读顺序是从右往左读,例如:
$$\left[\begin{matrix}1 & 2 & 3 \\4 & 5 & 6 \\7 & 8 & 9\end{matrix} \right]* \left[\begin{matrix}1\\2\\3\end{matrix} \right]$$ - 矩阵的几何概念可以理解为是描述变换的,包含旋转、缩放和平移等变换,其中旋转和缩放是线性变换,线性变换就是满足下面两个公式:$f(x)+f(y)=f(x+y)$,$kf(x)=f(kx)$,更具体的就是线性变换后的坐标系保持网格平行且等距分布,而平移则让原点发生了变换,被称为仿射变换,这也是为什么拓展成了4X4矩阵,多一个维度来表示平移,也就是所谓的齐次坐标。
上述的变换就可以通过一个统一的4X4矩阵表示出来:$$\left[\begin{matrix}M_{3*3} & t_{3*1} \\0_{1*3} & 1\end{matrix}\right]$$
左上角的矩阵$M_{3*3}$用于表示旋转和缩放,$t_{3*1}$用于表示平移,$0_{3*1}$表示零矩阵,右下角就是标量1。
按照书中的规定是先缩放,再旋转,最后平移,这个要理解需要再深入一点矩阵的几何概念,矩阵乘以向量的结果相当于将向量上面的坐标数值按照矩阵描述的坐标系来表示得到的向量,上面这句话有点绕,但是蛮重要的,不能理解的话建议去看看3Blue1Brown讲解线性代数的视频,里面很详细而且很专业hh,所以再回到上面顺序的问题,如果从原点先朝X轴方向平移5个单位,再放大2倍,在新放大的坐标系中,该点的坐标就变成了(10,0),实际上也就平移了10个单位,得到了错误的结果。
事实上如果用数学去验算也会发现如果不按照上述变换顺序来表示变换矩阵得到的结果和上面的矩阵结果也是不一样的。
在Unity多个旋转角度会按照zxy轴的顺序旋转。 - 两个不同坐标空间的坐标转换矩阵推导
$$ 设P坐标空间和C坐标空间 $$
$$ 则C坐标空间下A_c矢量转换到P坐标空间方程为:A_p=M_{c\rightarrow p}A_c $$
$$ P坐标空间下B_p矢量转换到C坐标空间方程为:B_c=M_{p \rightarrow c}B_p $$
$$ 已知:P坐标空间下C空间的原点以及3个坐标轴的向量表示分别为O_c,\vec X_c,\vec Y_c,\vec Z_c(一定要注意是P坐标空间下表示的) $$
$$ 设A_c坐标表示为(a,b,c)(注意该点是在C中的坐标系下的坐标),则易得A_p=Oc+a\vec X_c+b\vec Y_c+c\vec Z_c $$
$$ 设O_c为(x_{oc},y_{oc},z_{oc}),\vec X_c为(x_{xc},y_{xc},z_{xc}),\vec Y_c为(x_{yc},y_{yc},z_{yc}),\vec Z_c为(x_{zc},y_{zc},z_{zc}) $$
$$ A_p=(x_{oc},y_{oc},z_{oc})+a(x_{xc},y_{xc},z_{xc})+b(x_{yc},y_{yc},z_{yc})+c(x_{zc},y_{zc},z_{zc}) $$
$$ A_p=(x_{oc},y_{oc},z_{oc})+\left[\begin{matrix} x_{xc} & x_{yc} & x_{zc} \\y_{xc} & y_{yc} & y_{zc}\\z_{xc} & z_{yc} & z_{zc}\end{matrix}\right]*\left[\begin{matrix} a\\b\\c\end{matrix}\right] $$
$$ A_p=(x_{oc},y_{oc},z_{oc})+\left[\begin{matrix} | & | & | \\ \vec X_{c} & \vec Y_{c} & \vec Z_{c}\\| & | & |\end{matrix}\right]*\left[\begin{matrix} a\\b\\c\end{matrix}\right] $$
$$ A_p=\left[\begin{matrix} 1 & 0 & 0 &x_{oc}\\ 0 & 1 & 0 & y_{oc}\\0 & 0 & 0 & z_{oc}\\0 & 0 & 0&0\end{matrix}\right]*\left[\begin{matrix} | & | & |& 0 \\ \vec X_{c} & \vec Y_{c} & \vec Z_{c} &0\\| & | & | & 0\\0&0&0&1\end{matrix}\right]*\left[\begin{matrix} a\\b\\c\\1\end{matrix}\right] $$
$$ A_p=\left[\begin{matrix} | & | & |& x_{oc} \\ \vec X_{c} & \vec Y_{c} & \vec Z_{c} & y_{oc}\\| & | & | &z_{oc}\\0&0&0&1\end{matrix}\right]*\left[\begin{matrix} a\\b\\c\\1\end{matrix}\right] $$
$$ A_p=\left[\begin{matrix} | & | & |& | \\ \vec X_{c} & \vec Y_{c} & \vec Z_{c} &O_c\\| & | & | & |\\0&0&0&1\end{matrix}\right]*\left[\begin{matrix} a\\b\\c\\1\end{matrix}\right] $$
$$ 所以M_{c\rightarrow p}=\left[\begin{matrix} | & | & |& | \\ \vec X_{c} & \vec Y_{c} & \vec Z_{c} &O_c\\| & | & | & |\\0&0&0&1\end{matrix}\right],M_{p \rightarrow c}=M_{c\rightarrow p}^- $$
- 根据矩阵的性质我们可以得出如果这个转换矩阵为正交矩阵的话,那么它的逆矩阵就是它的转置矩阵。
这个实际应用在使用法线贴图并转换到世界坐标系中有很明显的体现,通过世界坐标下的法线向量和切线向量以及点的坐标求出切线空间转换到世界空间的矩阵,通过这种方式获取法线贴图中的法线信息。
坐标空间的变换
模型空间转换到世界空间
模型空间转换到世界空间的矩阵是根据Transform的数值通过计算得到的,计算的顺序和上述一样先缩放再旋转最后平移。
世界空间转换到观察空间
世界空间转换到观察空间(也叫做观察变换)是将坐标原点转换到摄像机,但是要注意观察空间是右手坐标系,可以认为在Unity中摄像机将它的Z轴取相反,在缩放矩阵中Z轴的数值采用-1,其他都是一样的。
观察空间转换到裁剪空间
观察空间转换到裁剪空间(Clip Space,也被称为齐次裁剪空间),这是为了方便裁剪顶点,为了投影做准备,转化的矩阵有两种。一个是透视投影的转换矩阵:
$$ M_{frustum}=\left[\begin{matrix} \frac {Cot\frac {FOV} 2} {Aspect} & 0 & 0 & 0 \\ 0 & Cot\frac {FOV} 2 & 0 & 0\\ 0 & 0 & \frac{Far+Near} {Far-Near} & -\frac{2*Near*Far} {Far-Near}\\ 0 & 0 &-1 & 0\end{matrix}\right] $$
$$ Aspect=\frac{nearClipPlaneWidth} {nearClipPlaneHeight} $$
$$ Aspect=\frac{farClipPaneWidth} {farClipPaneHeight} $$
Near是摄像机到达近裁剪平面的距离,Far是摄像机到达远裁剪平面的距离,FOV是视椎体竖直方向的张开角度。最后一行第三列的-1是很巧妙地将转换后的坐标W值变为原先坐标的-z值,然后判断xyz值是否都在[-w,w]的范围内来判断是否在视椎体内
最后变换后坐标系如图: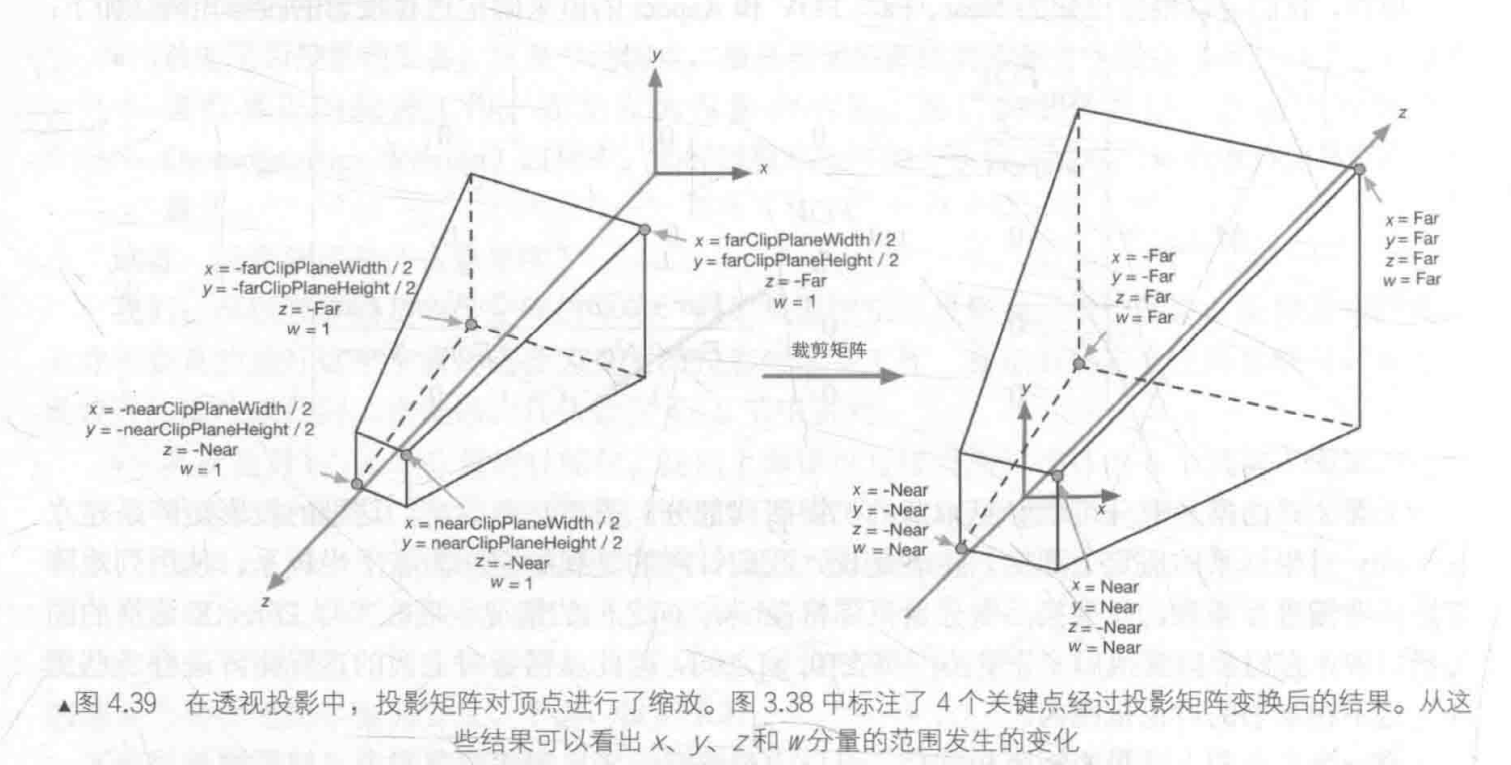
另一个是正交投影的投影矩阵:
$$ M_{frustum}=\left[\begin{matrix} \frac {1} {Aspect*Size} & 0 & 0 & 0 \\ 0 & \frac 1 {Size} & 0 & 0\\ 0 & 0 & -\frac{2} {Far-Near} & -\frac{Far+Near} {Far-Near}\\ 0 & 0 & 0 & 1\end{matrix}\right] $$
$$ Aspect=\frac{srcWidth}{srcHeight} $$
Near和Far是在摄像机中设置的,即摄像机分别距离近裁剪平面和远裁剪平面的距离。
Size也是在摄像机中设置的,相当于屏幕一半的高度。
然后判断xyz值是否都在[-1,1]范围内来判断是否在视椎体内。
最后变换后坐标系如图: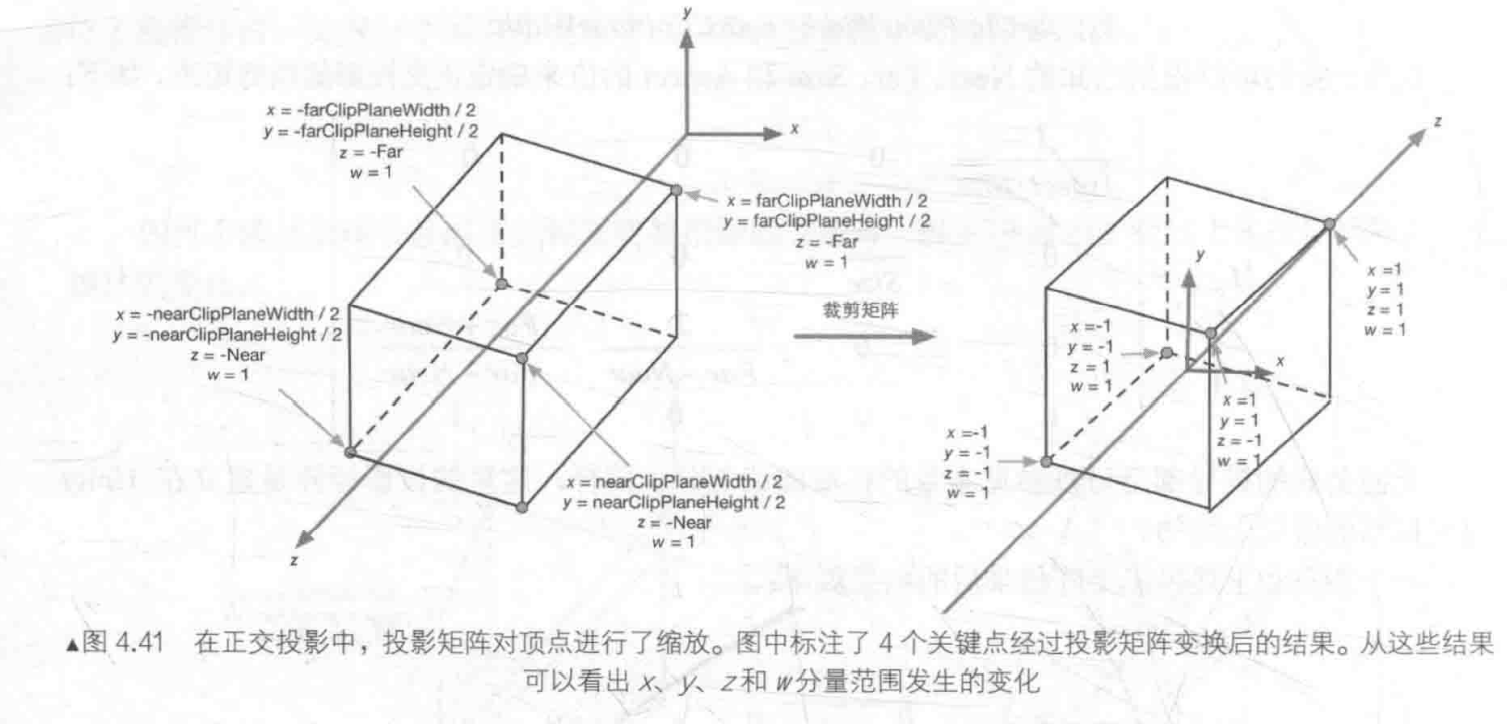
裁剪空间转换到NDC
裁剪空间转换到归一化的设备坐标(Normalized Device Coordinates,NDC,实际上就是下图的小方形),透视投影的裁剪空间转换到NDC坐标需要进行齐次除法(也叫透视除法,即xyz各个分量的值除以w),由于正交投影的w值是1,进行齐次除法并不会有什么变化。
透视投影裁剪空间转换到NDC: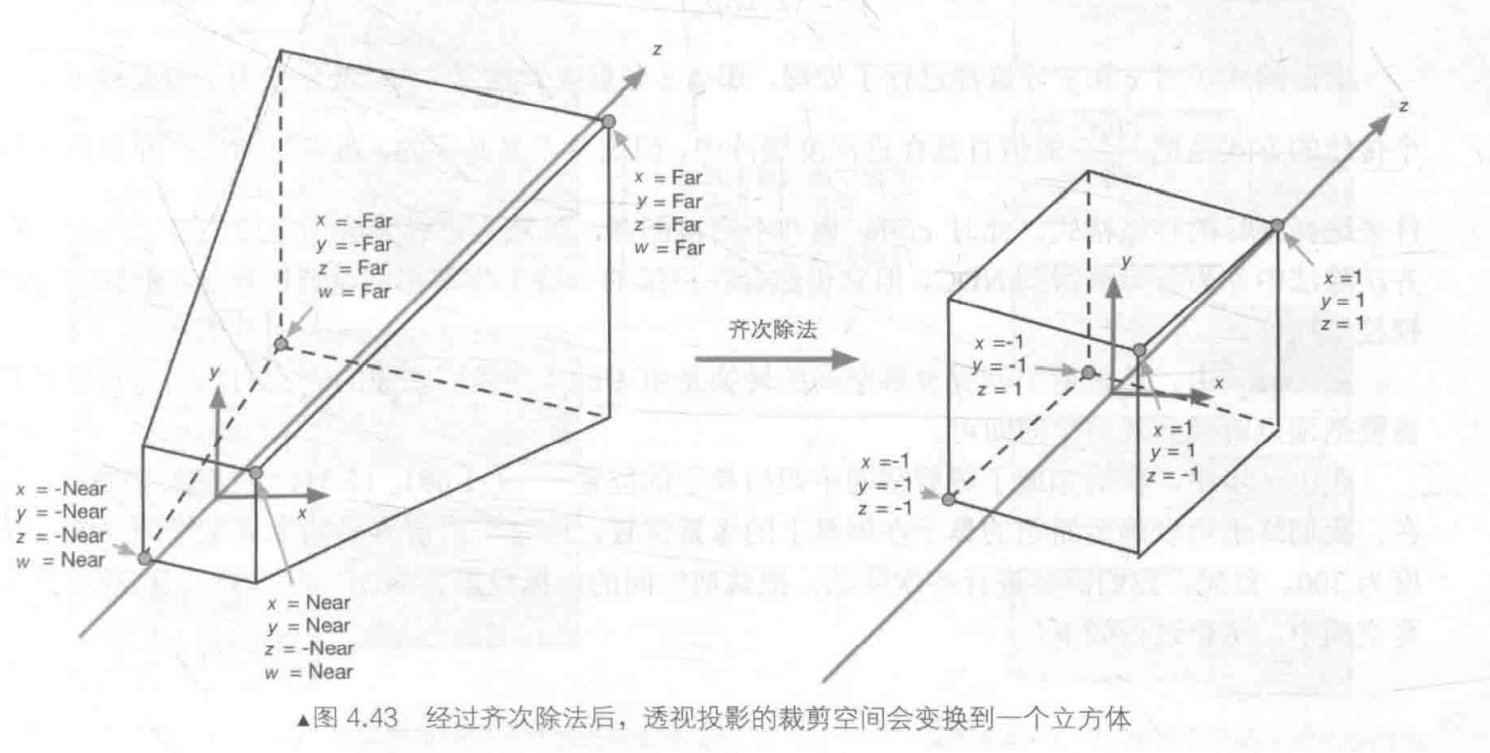
Unity选择的是OpenGL的齐次裁剪空间范围是[-1,1],但是DirectX中z的分量是[0,1],使用的时候要注意这个问题
NDC投影到屏幕空间
NDC投影至屏幕空间,屏幕空间是一个二维空间,左下角的像素坐标是(0,0),右上角的像素坐标为(pixelWidth,pixelHeight),转换公式为:
$srceen_x=\frac{clip_x*pixelWidth} {2*clipw}+\frac{pixelWidth}2\\srceen_y=\frac{clip_y*pixelHeight} {2*clipw}+\frac{pixelHeight}2$
z分量会被用于深度缓冲中,将$\frac{clip_z}{clip_w}$的值存入深度缓冲,但这并不是必须的
通过深度纹理坐标和屏幕纹理坐标倒推世界空间
通过深度纹理存储的深度值和屏幕纹理的uv值来获得世界空间的坐标算是蛮常用的,比如动态模糊效果中需要得到当前像素和上一次渲染像素的相对向量,下面是比较详细的推导。
假设当前像素对应深度纹理中的深度值为Depth
深度值的获取是需要对深度纹理的uv进行一些平台差异化处理,再在Shader中使用SAMPLE_DEPTH_TEXTURE(sampler, uv)函数获取屏幕纹理则通过脚本的OnRenderImage(RenderTexture src, RenderTexture dest,material)函数获取屏幕纹理通过上面两个纹理,可以得出NDC坐标系下的坐标:
$$ V_{ndc}=float4(src.uv.x*2-1,src.uv.y*2-1,Depth*2-1,1.0) $$
由于纹理保存数据以及uv的数值范围是[0,1],所以得到NDC坐标需要上面的转换,即将范围转换为[-1,1]
NDC逆推到裁剪空间
$$ V_{clip}=V_{ndc}*V_{clip}.w $$
虽然这里我们并不知道V_{clip}.w,但我们可以先留着
裁剪空间逆推到观察空间:
$$ V_{view}=M_{view \rightarrow clip}^-V_{clip} $$
观察空间转换到世界空间:
$$ V_{world}=M_{world \rightarrow view}^-V_{view} $$
通过上面的式子我们可以得出:
$$ V_{world}=M_{world \rightarrow view}^-V_{view}=M_{world \rightarrow view}^-M_{view \rightarrow clip}^- $$
$$ V_{clip}=(M_{view \rightarrow clip}M_{world \rightarrow view})^-V_{clip} $$
$$ V_{world}=(M_{view \rightarrow clip}M_{world \rightarrow view})^-V_{ndc}*V_{clip}.w $$
现在就剩下$V_{clip}.w$需要知道了,但事实上我们知道$V_{world}.w$为1,则得到:
$$ V_{world}.w=((M_{view \rightarrow clip}M_{world \rightarrow view})^-V_{ndc}).w*V_{clip}.w=1 $$
$$ V_{clip}.w=\frac{1}{((M_{view \rightarrow clip}M_{world \rightarrow view})^-V_{ndc}).w} $$
所以最后$V_{world}$则等于:
$$ V_{world}=\frac{(M_{view \rightarrow clip}M_{world \rightarrow view})^-V_{ndc}}{((M_{view \rightarrow clip}M_{world \rightarrow view})^-V_{ndc}).w} $$
这也是为什么得出的结果需要除以自身的$w$的原因(之前半天没搞懂,列一列就知道了hh)
参考:
-《Shader入门精要》
-3Blue1Brown讲解线性代数的视频