PBR理论基础-1
《PBR理论基础-1》里面整理了辐射度量学的基本概念以及BRDF推导出的渲染方程。
辐射度量学
辐射度量学是对光照的一套测量系统和单位,它能够准确的描述光线的物理性质。
下面是里面的基础概念
- 辐射能量(Radiant energy),指电磁辐射的能量,一般用大写的Q表示,单位是焦耳J。
- 辐射通量(Radiant flux),指单位时间辐射出的能量,一般用$\Phi$表示,下方是和辐射能量的公式:
$$\Phi=\frac {dQ}{dt}$$ - 辐射强度(Radiant intensity),指单位立体角由某一光源发出的功率,一般用大写的I表示,单位是SI(法语:Système International d'Unités),下方是和辐射通量的公式:
$$I(w)=\frac {d\Phi}{dw}$$
这里又会有一个问题,什么是单位角?首先要知道什么是立体角,就是对二维圆向三维球拓展的角。
首先考虑一下二维的角是什么?
通过弧度制我们可知,角可表示为弧长与半径的比值,圆的弧度值就是2$\pi$。
那么立体角已经呼之欲出了,就是投影面积与半径平方的比值,球的立体角值就是4$\pi$,立体角用$\Omega$表示,公式如下:
$$\Omega=\frac {A}{r^2}$$
按照上述公式,单位角也就可以得出:
$$dw=\frac {dA}{r^2}$$
现在就是求出单位面积的问题,通过下方的图可得出: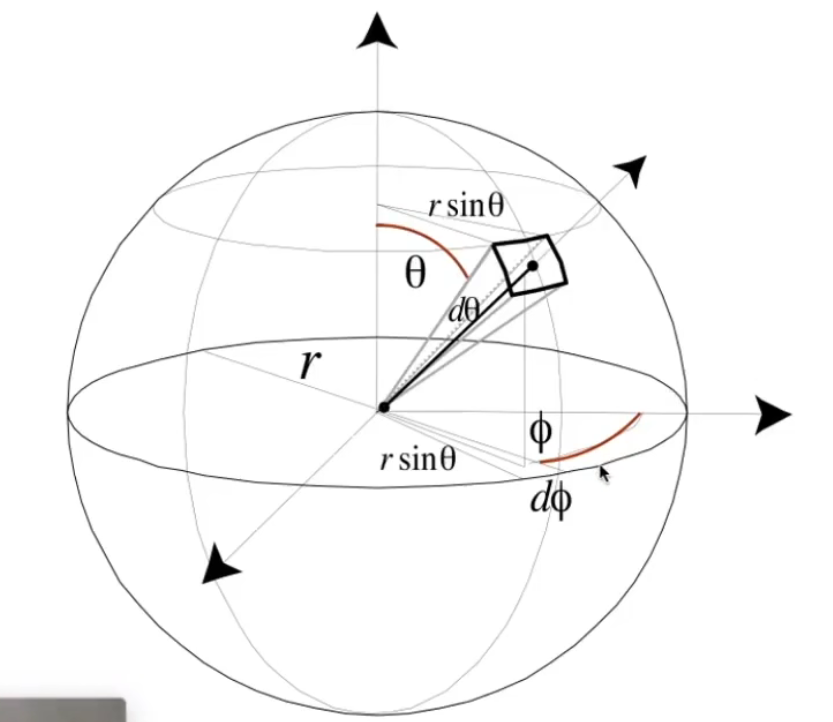
$$dA=(r\sin\theta d\phi)*(rd\theta)=r^2\sin\theta d\theta d\phi$$
$$dw=\frac {dA}{r^2}=\sin\theta d\theta d\phi$$
其实通过上图可以知道,当确定了$\theta$和$\phi$,我们便获得了一个方向,称它为$w$,然后在此微分,计算得出$dw$,这样就能知道辐射强度(Radiant intensity),即可以表示某方向上光源亮度。
但如果是各项同性点光源,那么它所有方向上的亮度都与方向无关,即都是相同亮度的,则可以直接除以$4\pi$,得出$I=\frac {\Phi}{4\pi}$。 - 辐照度(irradiance),指的是单位面积入射到表面上一点的辐射通量,一般用大写的E表示,单位为lux(照度,勒克斯),公式如下,$X$在某点的辐照度和辐射通量:
$$E(X)=\frac {d\Phi(X)}{dA}$$
兰伯特余弦定律(表面辐照度与光方向和表面法线夹角的余弦值成正比),要在前面多乘以一个余弦值,和高中某些知识很相似。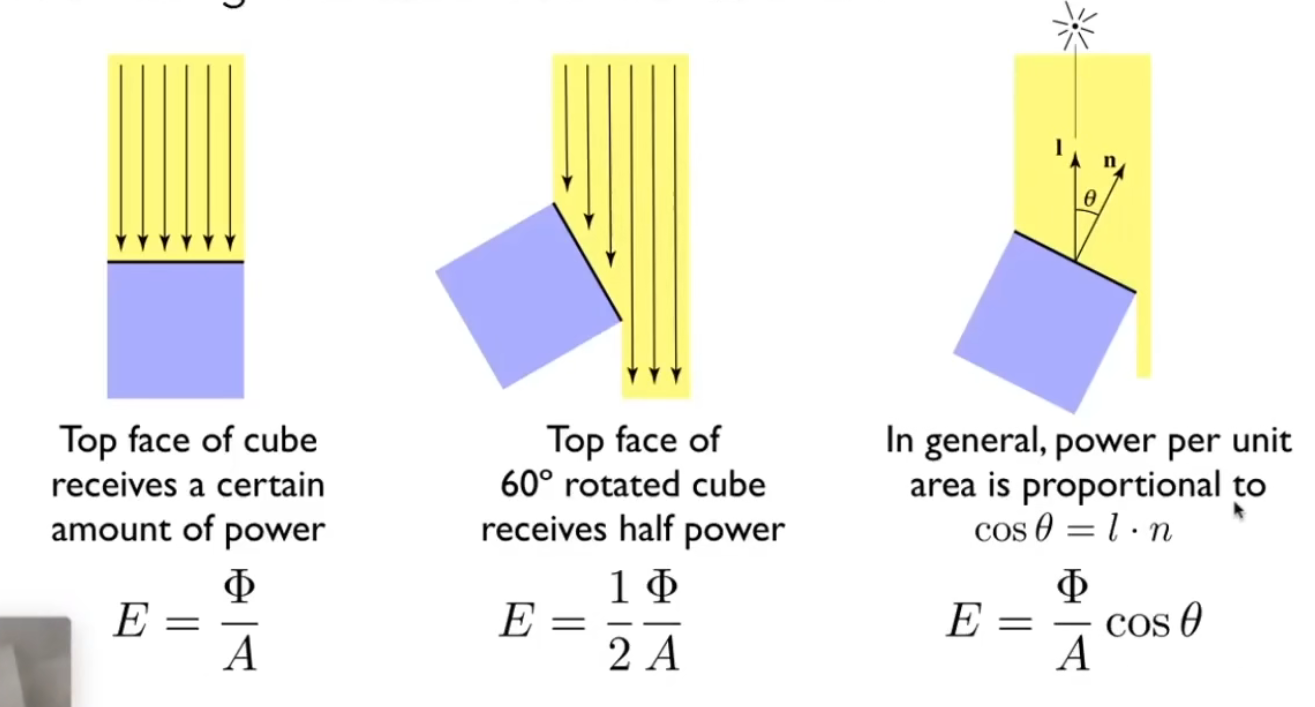
辐照度衰减,这个很好理解,现实生活中光越远肯定越弱,这个越弱是远处的点辐射度在衰减,假设光发射的辐射通量为$\Phi$且假设光发射的辐射通量在一个均匀的角分布,某点距离它$r$,则该点的辐射度$E$为:
$$E=\frac {\Phi}{4 \pi r^2}$$
关于为什么是r的平方,B站的一个视频很生动,不理解可以去看看。 - 辐射(radiance),描述光在环境中的分布的基本场景,与光线有关,即描述光线传播的一些属性,我们渲染的时候就是计算关于辐射的。
辐射(radiance),也称为亮度(luminance),指在一个表面在每单位立体角、每单位投影面积上所发射(emitted)、反射(reflected)、透射(transmitted)或接收(received)的辐射通量(功率),单位为尼特,公式如下:
$$L(p,w)=\frac {d^2\Phi(p,w)}{dwdA\cos \theta}$$
描述辐射的图如下: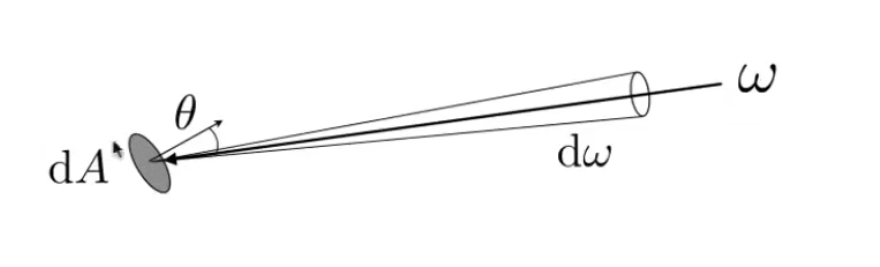
辐射包含两个:
入射辐射(Incident Radiance),指到达表面的单位立体角的辐照度。即它是沿着给定光线到达表面的光(入射方向指向表面,公式如下:
$$L(p,w)=\frac {d E(p)}{dw\cos \theta}$$
出射辐射(Exiting Radiance),指离开表面的单位投影面积的辐射强度。例如:对于面光(area light),它是沿着给定光线发射的光(出射方向指向表面),公式如下:
$$L(p,w)=\frac {dI(p,w)}{dA\cos \theta}$$
这样就与之前的两个概念联系起来了。
双向反射分布函数(BRDF)
现在我们可以通过上面概念的基础上来描述反射这一现象,已知某点在接受到某一方向的亮度($dE(w_i)$)后会朝不同方向把能量反射出去($dL_r(x,w_r)$)。
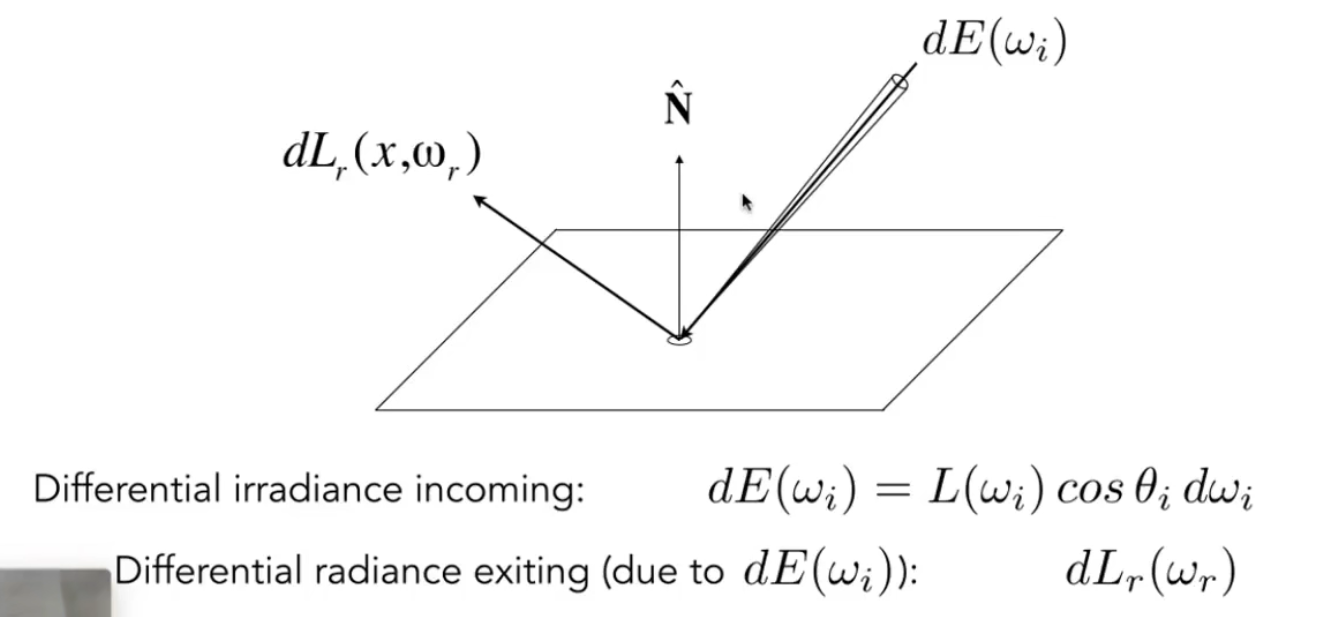
不同的材质反射的能量分布不同,像理想镜面反射能量完全朝反射方向发出,像粗糙平面就会均匀的反射所有方向(漫反射)。
BRDF就是描述一个方向入射反射到另一个方向的比例。
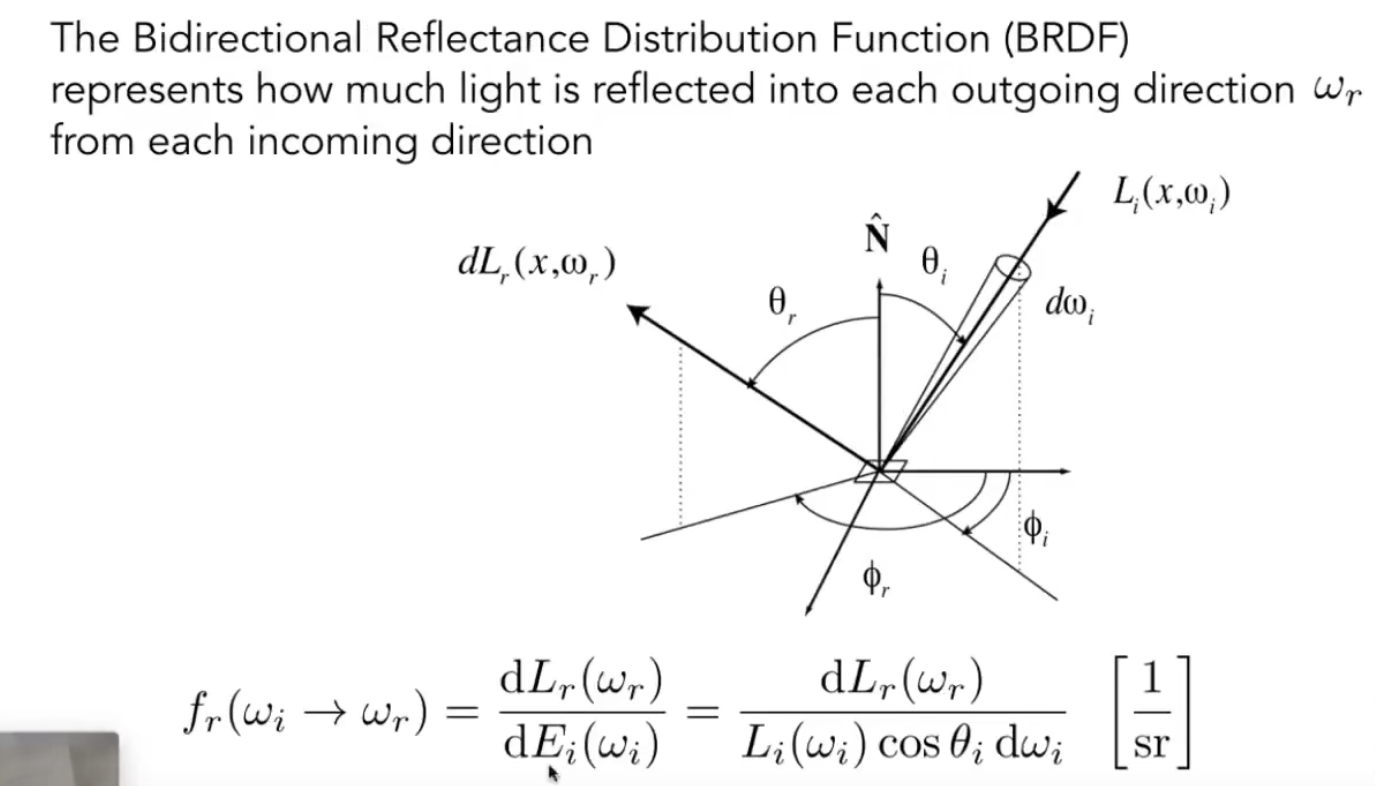
这样我们就可以计算某一点的反射到某一方向的能量。
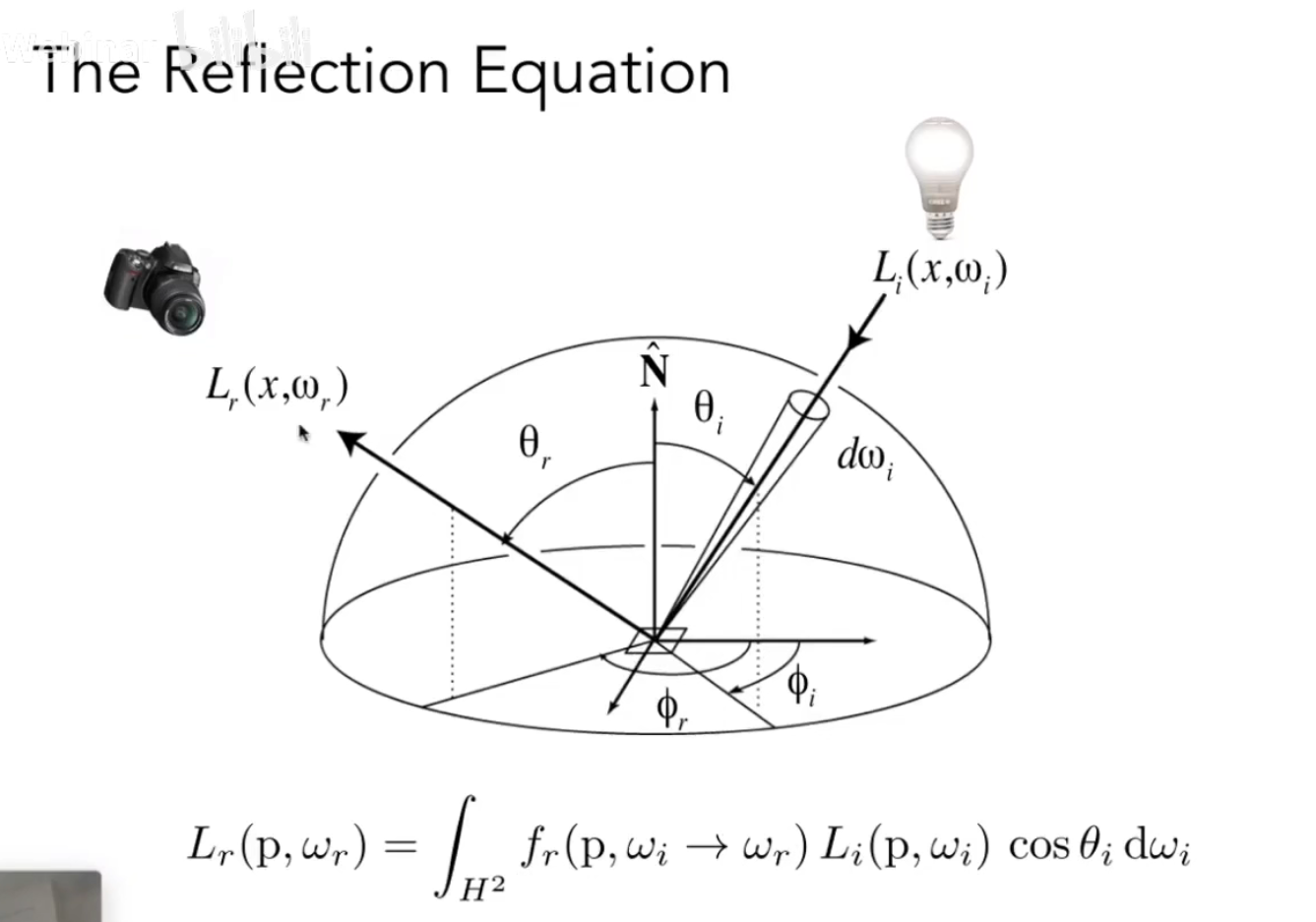
这里的光源不只是光源,还有其他物体发出的光线,是一个递归的过程,和Ray Tracing很相似。
在上述的基础我们就可以得到一个渲染方程:
$$ L_o(p,w_o)=L_e(p,w_o)+\int_{\Omega+}L_i(p,w_i)f_r(p,w_i,w_o)(n*w_i)dw_i $$
这里多加了一个自发光,$\cos\theta $转换成为$n*w_i$,其他和之前一样。
实际写过Unity的前向渲染的都知道在处理不同光照类型是需要多一个Pass来处理的,但是上面的方程直接将所有的都涵盖了,包括点光源,面光源以及其他物体的反射等,对其他物体的反射是需要再计算的,相当于一个递归的过程,递归的深度越深,效果越真实。
在GAMES101-现代计算机图形学入门P15后面47分左右后面还有推导,这里就不继续写了。