PBR理论基础-4
本篇文章将介绍IBL技术并在Unity中实现
IBL(Image-Based Lighting)
我们先回顾一下之前的渲染公式:
$$ L_o(p,w_o)=L_e(p,w_o)+\int_{\Omega+}L_i(p,w_i)f_r(p,w_i,w_o)(n*w_i)dw_i $$
我们要计算某点的亮度是需要对周围的辐照度进行球面积分,但是实际上我们不仅仅需要计算直接光源辐照度,还需要计算其他物体辐照度,其他物体也需要自己进行积分计算自己的亮度,是一个递归过程,在实时渲染中这种计算量实在太大了,所以这里就有大佬想出了IBL的方式近似模拟间接光照,实现全局光照(直接光照+间接光照)。
IBL主要思路可以通过名字得知,基于图片的光照,它通常使用Cubemap事先记录周围环境贴图,进行预处理后,在渲染时采样。
我们将之前渲染公式忽略自发光并拆分一下:
$$ L_o(p,w_o)=\int_{\Omega}(k_d\frac{c}{\pi})L_i(p,w_i)(n*w_i)dw_i+\int_{\Omega}(\frac {FGD} {4(n*w_i)(n*w_o)})L_i(p,w_i)(n*w_i)dw_i $$
现在IBL被拆解成两个部分,分别是间接光漫反射部分和间接光镜面反射部分,也就是加号左边和右边的式子。
间接光漫反射部分
辐照度贴图(Irradiance MAP)
对于漫反射的部分通常采用获取预处理过的环境贴图采样,这种预处理后的贴图叫做辐照度贴图(Irradiance map)。
先讲的简单容易理解一些,假设要计算一个点的辐照度,那么我们可以很容易得出就是一个半球上所有的辐射值之和,半球则是通过该点上的法线决定了,如下图,具体获得间接光漫反射的辐射度,我们需要计算半球上所有采样方向$w_i$,并对其采样结果进行卷积后,输出$w_0$的辐射度结果。
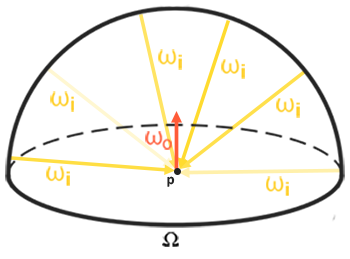
通过蒙特卡洛法我们可以求解出大致的积分结果,下面的伪代码帮助理解辐照度贴图的生成过程:
//vec3Array里面存的是p点半圆随机取的一组方向向量
foreach(vec3 in vec3Array)
{
sum += SampleCube(CubeMap,vec3)
}
//将所有随机采样值取平均后存入IrradianceMap
IrradianceMap.SetValue(sum/vec3.Count,Normal) 通过上述的步骤我们就可以通过环境贴图得到一张辐照度贴图,但是在实际的计算机图形学中,我们只需要视觉效果上接受就可以了,所以采用蒙特卡洛法是用一种使用低差异序列生成蒙特卡洛样本向量的有偏的(样本不是完全随机,而是集中于特定的值或方向)拟蒙特卡洛积分,通过这种方法生成的样本具有更快的收敛速度(也就是重要性采样)。

但是在实际的游戏运用中不可能只通过一张环境贴图就能实现一个场景的间接光,通常需要多个贴图进行插值得到结果。
LightProbe 与 球谐函数
在Unity里面是通过LightProbe来存储环境辐照度,但它并不是通过辐照度贴图来存储,而是用球谐函数存储对应信息,存储的是球谐函数的9个参数。
对于球谐函数并不是很了解,打算之后学习后详细的写一篇文章来叙述,这里就讲一下怎么实际运用,首先在场景中放入LightProbe并烘焙,之后就在shader代码通过Unity函数获得间接光漫反射。
//通过ShaderSH9获得间接光漫反射辐照度
//注意Tags{ "LightMode"="ForwardBase"} 才能正确得到函数值
//否则ShadeSh9返回值为0
float3 irradianceSH = ShadeSH9(float4(worldNormal,1));
//乘以光照颜色以及Kd
float3 Diffuse_Indirect = irradianceSH * _Color *KD_IndirectLight;按照上面的代码就可以得到间接光漫反射。
间接光镜面反射部分
镜面反射部分会比漫反射复杂一点,原因看下方公式:
$$ L_o(p,w_o)=\int_{\Omega}\frac {FGD} {4(n*w_i)(n*w_o)}L_i(p,w_i)(n*w_i)dw_i=\int_{\Omega}f_r(p,w_0,w_i)L_i(p,w_i)(n*w_i)dw_i $$
将积分中函数整合后,发现镜面部分受到两个参数的影响,不像漫反射部分仅受$w_i$入射光反向的影响,而是不仅受$w_i$入射光的影响,而且还收到$w_o$视角方向的影响,所以如果积分所有结果数据量会非常庞大,这显然很难实时计算,Epic Games提出了一种解决方案叫分割求和近似法(split sum approximation),这里的分割就是将镜面反射积分分为两个独立的积分:
$$ L_o(p,w_o)=\int_{\Omega}L_i(p,w_i)dw_i*\int_{\Omega}f_r(p,w_0,w_i)n*w_idw_i $$
第一部分
$$ L_o(p,w_o)_{IndirectLightPart1}=\int_{\Omega}L_i(p,w_i)dw_i $$
卷积的第一部分成为预滤波环境贴图,在微观尺度上,表面越粗糙,反射越模糊,因为表面取向与整个宏观表面取向的偏离更强,如下图: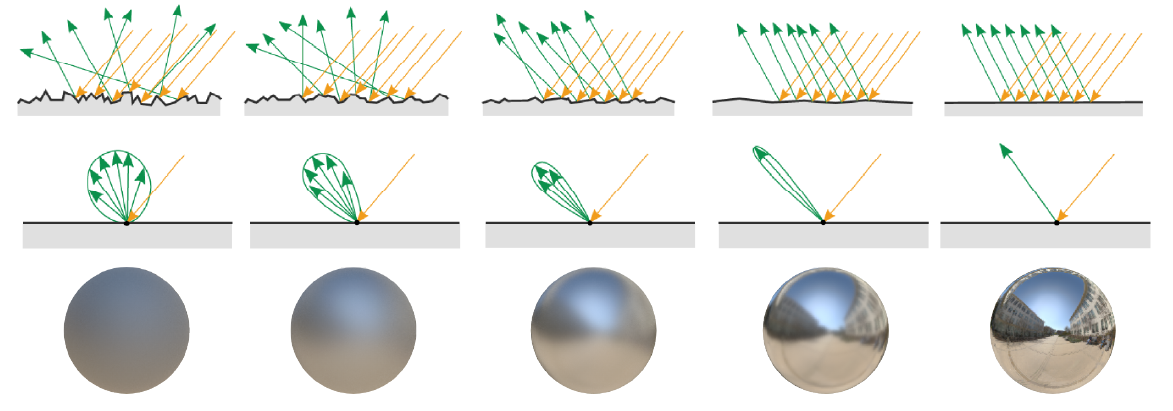
粗糙度越小,积分环境贴图卷积核面积越小,中心权重越大,反射效果越清晰,于是根据粗糙度分LOD等级,预先根据等级计算结果,得到具有不同LOD等级的预滤波环境贴图,如下:

在Unity里面获得预滤波环境贴图,是通过ReflectionProbe烘焙并存储的,ReflectionProbe会将周围场景信息保存到CubeMap中,当把ReflectionProbe放在场景中烘焙后,物体会获取最近的ReflectionProbe中的信息,通过unity_SpecCube0这个变量在代码中得到,将粗糙度转换为mip后,从该贴图中获取,代码如下:
//将粗糙度转换为mip
fixed mip = _Roughness * (1.7 - 0.7 * _Roughness) * UNITY_SPECCUBE_LOD_STEPS;
//根据mip以及反射方向采样贴图
float4 rgb_mip = UNITY_SAMPLE_TEXCUBE_LOD(unity_SpecCube0,worldReflect,mip);
//注意这里还要使用DecodeHDR将HDR格式转为RGB格式
fixed3 EnvSpecularPrefilted = DecodeHDR(rgb_mip, unity_SpecCube0_HDR);第二部分
BRDFLut
$$ L_o(p,w_o)_{IndirectLightPart2}=\int_{\Omega}f_r(p,w_0,w_i)n*w_idw_i $$
首先先讲一个细节,就是$f_r$中包含G函数,之前介绍G函数中直射光和IBL的k值是不同的,具体可以查看我的第二篇文章最后介绍G函数的部分。
这个部分并没有$L_i(p,w_i)$,所以考虑的就是在纯白的环境光下对镜面BRDF积分,其中的变量包含$n*w_i$,表面粗糙度, 菲涅尔系数$F_0$这三个,在一系列变换后可以得到下面这个式子,变换过程可以查看参考4的预计算BRDF部分:
$$ F_0\int_\Omega{f_r(p,w_0,w_i)(1-(1-w_0*h)^5)n*w_i}dw_i+\int_\Omega{f_r(p,w_0,w_i)(1-w_0*h)^5n*w_i}dw_i $$
$F_0$菲涅尔系数与之前直接光计算不同,之前是通过n和h来计算,而间接光是通过n和v来计算。
和之前计算卷积类似,现在是输入$n$和$w_i$的夹角以及表面粗糙度,并将结果存储到2D查找纹理(Look Up Texture,LUT)中的RG通道中,这张纹理被称为BRDF积分贴图,X轴为夹角,Y轴为表面粗糙度,如下图:

R通道存储的加号左边的积分结果,G通道存储的加号右边的积分结果,接下来我们需要这个积分值就可以直接通过坐标获取。
在Unity中得到LUT的结果可以通过下方代码实现:
float2 env_brdf = tex2D(_BRDFLUTTex, float2(n_dot_v,_Roughness)).rg;数值拟合
第二部分的结果还可以通过数值拟合的方式来实时计算,效果比Lut更好,更节省性能,详细的信息可以查看参考5的文章的数值拟合部分,在项目里的实现我直接照搬了文章的函数。
代码实现间接光部分
在Github项目里面的MyPBR.shader就是最终结合了直接光和间接光的Shader,在项目里面使用需要注意在场景中添加LightProbe和ReflectionProbe并烘焙,否则效果会有问题,如果有帮助请点个Star,Thanks♪(・ω・)ノ。
参考
- 基于物理的渲染:基于图像照明(Image-based Lighting)
- 《Adopting a physically based shading model》,比较细致的文章吗,其中介绍了处理间接光时为什么多加一个粗糙度因子来修改F函数让渲染更能符合菲涅尔衰减的现象(fresnel attenuation)
- learnopengl的漫反射辐照度章节
- learnopengl的镜面反射IBL章节
- 光照模型 PBR
- IBL推导及实现,数学推导IBL,我看不懂但大受震撼,有能力的可以去看看