PBR理论基础-3
本篇将对上文进行一些补充以及根据之前的理论在unity中实现直射光PBRShader。
反射方程中的漫反射项
上文讲到Cook-Torrance模型中的方程如下面的式子:
$$ f_r=k_df_{diffuse}+k_sf_{specular} $$
其中提到$k_d$与$k_s$相加等于1,这主要是因为当时只考虑到漫反射和镜面反射,实际上应该比1还要小(比如折射吸收后造成的能量损失),下面列出更加正确的漫反射项:
$$ k_d=(1-k_s)(1-_Metallic) $$
其中_Metallic表示物体的金属程度,当金属程度越高,那么它的漫反射越小。
D函数
法线分布函数实际上在Blinn-Phong中的高光模型中就实现过,即$D(h)=(n*h)^{gloss}$,只不过GGX(Trowbridge-Reitz)能够更好地根据PBR模型中的粗糙度来计算出更好效果的高光长尾。
F函数
上文在最后F函数中提到了:
$$ F_0=lerp(0.04,\rho,metalness) $$
首先了解什么是F0,它表示当光线垂直(以0度角)撞击表面时,该光线被反射(Reflected)为镜面反射光的比率,通常我们用F0表示材质的特征反射率。
在实际的物理中F0应表示为:
$$ F_0=(\frac {n_1-n_2}{n_1+n_2})^2 $$
n1,n2分别两种介质的折射率,但已经有人给我们总结好每个材质在空气中(注意是空气中,即n1为1,如果是其他介质则需要重新计算)的F0值,比如《Real-Time Rendering 4th》中就有PBR材质F0反射率速查图表:
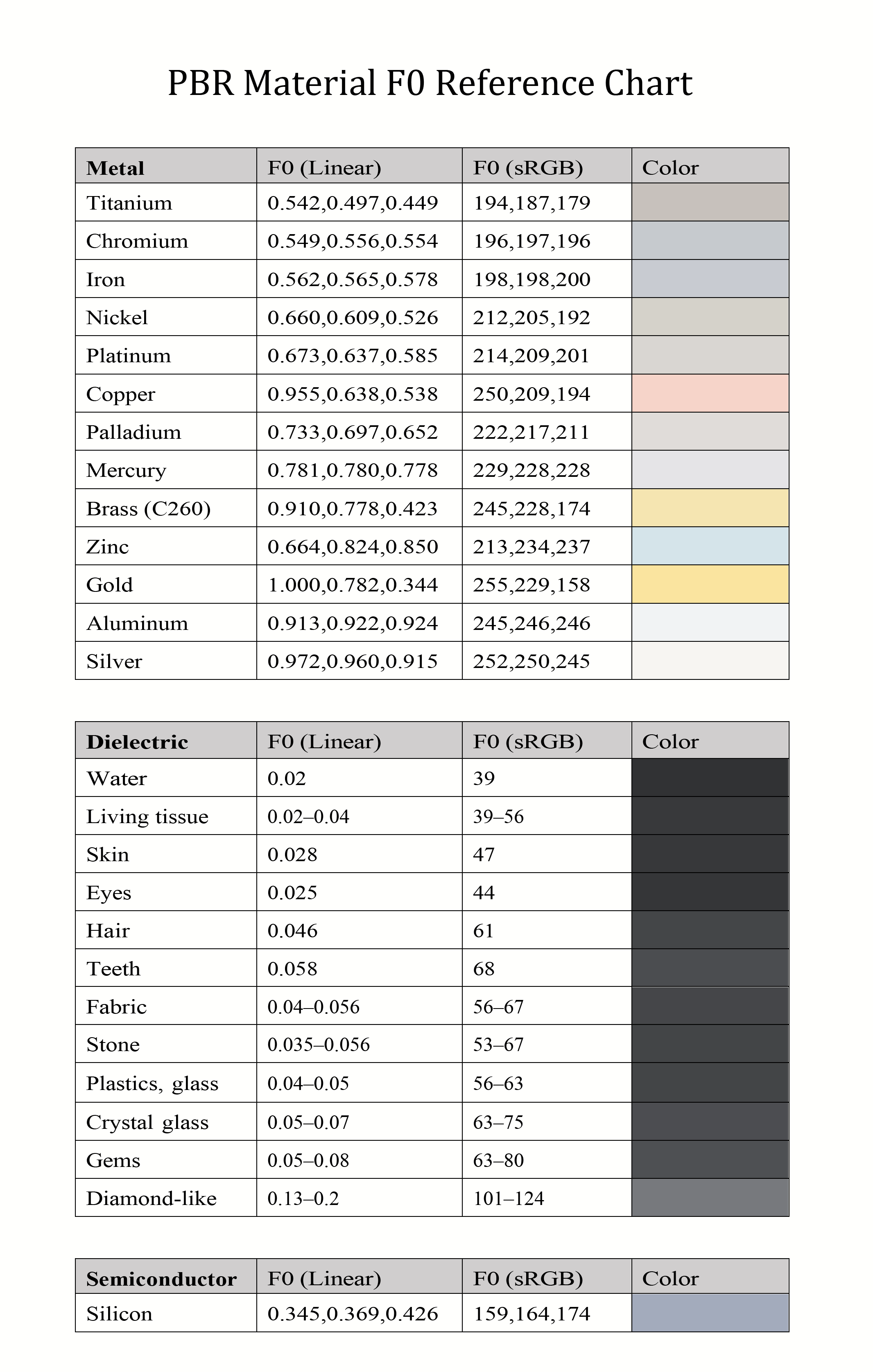
上图单纯放出来给大家瞧瞧,在实际编码时会采用一开始列的式子作为简化,想要具体了解可以查看《基于物理的渲染(PBR)白皮书 》第二篇文章以及它的Reference。
G函数
文中提到了k值,它是粗糙度基于几何函数是针对直接光照还是针对IBL光照的重映射(Remapping),所以两种光照中k值不同,我是从LearnOpenGL这篇文章中看到的,具体的推导和原因我不是很清楚,有兴趣可以百度。
有些文章中会将G函数和校正因子写在一起,作为V函数(可见性)表示,实质上是一样的,注意即可。
Unity实现直射光PBRShader
注意,这里写出的PBR模型仅作为学习使用,许多地方都是极简版,如果真要用PBR材质可以直接用内置的Standard材质。
对于由于是极简化的,所需要的属性仅有三个,即物体表面颜色,粗糙度和金属程度:
Properties
{
_Color ("Color", Color) = (1,1,1,1)
_Roughness("Roughness",Range(0.02,1))=0.5
_Metallic("Metallic",Range(0,1))=0.5
}首先根据之前文章列出我们的D、F、G函数,这里采用的函数都是上文提到过的,原原本本的抄下来就好了:
CGINCLUDE
#include "UnityCG.c
#include "AutoLight.cginc"
//D函数,采用GGX
fixed D_GGX(fixed3 n,fixed3 h,fixed roughness)
{
fixed a=roughness*roughness;
fixed denom= pow(saturate(dot(n,h)),2)*(a*a-1)+1;
return a*a*UNITY_INV_PI/(denom*denom+1e-5f);
}
//F函数,采用Schlick的Fresnel近似
fixed3 F_Schlick(fixed3 F0,fixed3 v,fixed3 h)
{
return F0+(1-F0)*pow(1-saturate(dot(v,h)),5);
}
//G函数,采用Schlick-GGX
fixed G_Part_Schlick_GGX(fixed3 n,fixed3 v,fixed k)
{
return saturate(dot(n,v))/((1-k)*saturate(dot(n,v))+k);
}
fixed G_Schlick_GGX(fixed3 n,fixed3 l,fixed3 v,fixed roughness)
{
fixed k=pow(roughness+1,2)/8;
return G_Part_Schlick_GGX(n,v,k)*G_Part_Schlick_GGX(n,l,k);
}
ENDCG如果要计算上述函数,我们还需要物体的顶点坐标来获取世界坐标系下的光线向量(l表示),法线向量(n表示),视线方向(v表示),半矢量法线(h表示,即normalize(l+v)),这些都是基础中,不会的可以阅读《Unity Shader入门精要》学习(打好基础先)。
在片元着色器中根据函数的参数正确放入,计算出各个函数的值,并得到最终结果。
//F0
fixed3 F0=lerp(0.04,_Color,_Metallic);
//D、F、G函数结果
fixed D=D_GGX(worldNormal,h,_Roughness);
fixed3 F=F_Schlick(F0,worldViewDir,h);
fixed G=G_Schlick_GGX(worldNormal,worldLightDir,worldViewDir,_Roughness);
//根据F和金属值计算kd
fixed3 kd=(1-F)*(1-_Metallic);
//漫反射
fixed3 diffuse=_Color*kd/UNITY_PI;
//镜面反射
//分母加上1e-5f避免除0
fixed3 specular=F*D*G/(4*saturate(dot(worldNormal,worldLightDir))*saturate(dot(worldNormal,worldViewDir))+1e-5f);
//最终直射光得到结果
fixed3 directLight=(diffuse+specular)*_LightColor0.rgb*saturate(dot(worldNormal,worldLightDir));这里最后漫反射和镜面反射相加后还需要乘以一个法线和光线向量的点乘,这里可以回顾一下第一章的兰伯特余弦定律就能够理解了。
这里是完全根据之前的函数来计算的,但是很明显可以发现点乘的计算重复了很多次,所以可以将之前的函数进行修改,将参数修改为点乘的结果而不是两个向量,然后在片元着色器中先计算出各个向量点乘的结果再传入到方法中,能够提高代码效率。
这里就不再贴代码了,文章最后会将两种Shader都放到Github有需要的可以自行查看。
Disney Principled BRDF的着色模型
Disney根据自己的观察得出结论(详细的内容可以查看基于物理的渲染(PBR)白皮书 第三章以及Reference),创建了自己的BRDF模型:
$$ f(l,v)=diffuse+\frac {F(l,h)G(l,v)D(h)} {4(n*l)(n*v)} $$
镜面反射项与之前的是一样的,主要是漫反射项。
Disney表示Lambert漫反射模型在边缘上通常太暗,而通过尝试添加菲涅尔因子以使其在物理上更合理,但会导致其更暗,所以它开发了一种用于漫反射的新的经验模型,以在光滑表面的漫反射菲涅尔阴影和粗糙表面之间进行平滑过渡。
思路方面,Disney使用了Schlick Fresnel近似,并修改掠射逆反射(grazing retroreflection response)以达到其特定值由粗糙度值确定,而不是简单为0。
Disney Diffuse漫反射模型的公式为:
$$ F_{D90}=0.5+2roughness\cos^2\theta_d $$
$$ diffuse=\frac{baseColor}\pi(1+(F_{D90}-1)(1-\cos\theta_l)^5)(1+(F_{D90}-1)(1-\cos\theta_v)^5) $$
其中$\theta_d$为光线向量与半矢量法线(h)的夹角(有的代码中计算是把光线向量改用视线方向,实际上是一样的),$\theta_l$为法线和光线向量的夹角,$\theta_v$为法线和视线方向的夹角。
在Unity中的代码就是:
//Disney漫反射代码
float DisneyDiffuse(float roughness, float v_dot_h, float n_dot_l, float n_dot_v)
{
float fd90 = 0.5 + 2 * roughness * v_dot_h * v_dot_h;
float NdotLSqr = n_dot_l * n_dot_l;
float NdotVSqr = n_dot_v * n_dot_v;
float fd = 1.0 *UNITY_INV_PI * (1 + (fd90 - 1) * NdotLSqr * NdotLSqr * n_dot_l) * (1 + (fd90 - 1) * NdotVSqr * NdotVSqr * n_dot_v);
return fd;
}
//片元着色器代码
fixed3 diffuse =_Color*DisneyDiffuse(_Roughness, v_dot_h, n_dot_h, n_dot_v);
//勘误,上面代码我在实现完间接光之后发现漫反射过于强烈,效果不对有问题
//在查看完Disney源码后才发现它最后还乘以了(1-_Metallic),所以这个公式计算出的结果相当于替换了之前的(1-F)
diffuse*=(1-_Metallic);最后效果和之前差不多,左边是Lambert,右边是Disney:
参考
- LearnOpenGL
- 《Unity Shader入门精要》
- 基于物理的渲染(PBR)白皮书
- 光照模型PBR,知乎上的一篇文章,很多光照模型都在其中列举出来