PBR理论基础-2
《PBR理论基础-2》介绍了微平面理论以及Cook-Torrance BRDF的推导
微平面理论(microfacet theory)
在白皮书中描述的是:
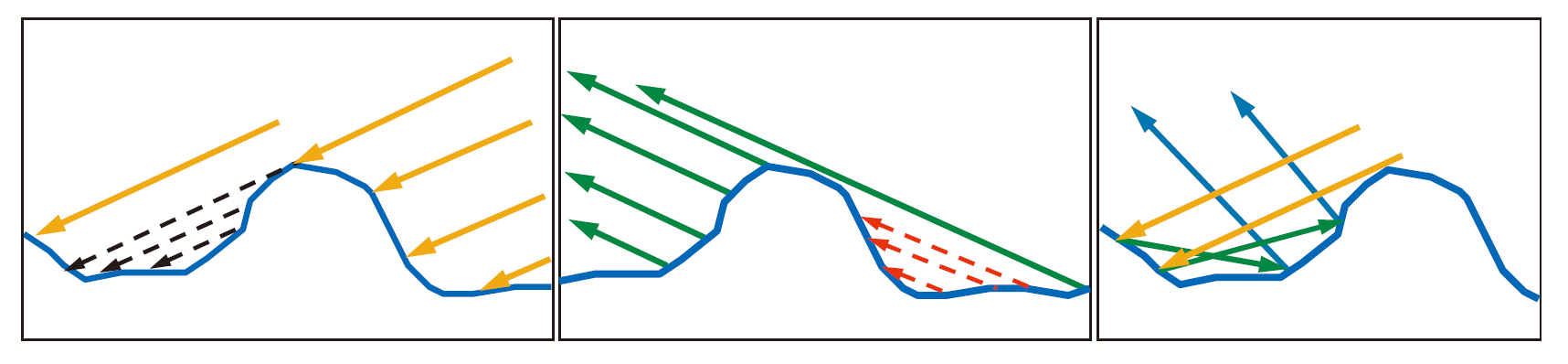
光在与非光学平坦表面(Non-Optically-Flat Surfaces)的交互时,非光学平坦表面表现得像一个微小的光学平面表面的大集合。表面上的每个点都会以略微不同的方向对入射光反射,而最终的表面外观是许多具有不同表面取向的点的聚合结果。
我在到处找了关于非光学平坦表面(Non-Optically-Flat Surfaces)和光学平面表面的概念,不管是哪里都没有,这里就暂且理解为物体表面和理想镜面好了。
注意我们原本物体的法线是所有微平面的平均表面法线。
这种微小理想镜面法线越杂乱,它的物体表面就越粗糙。
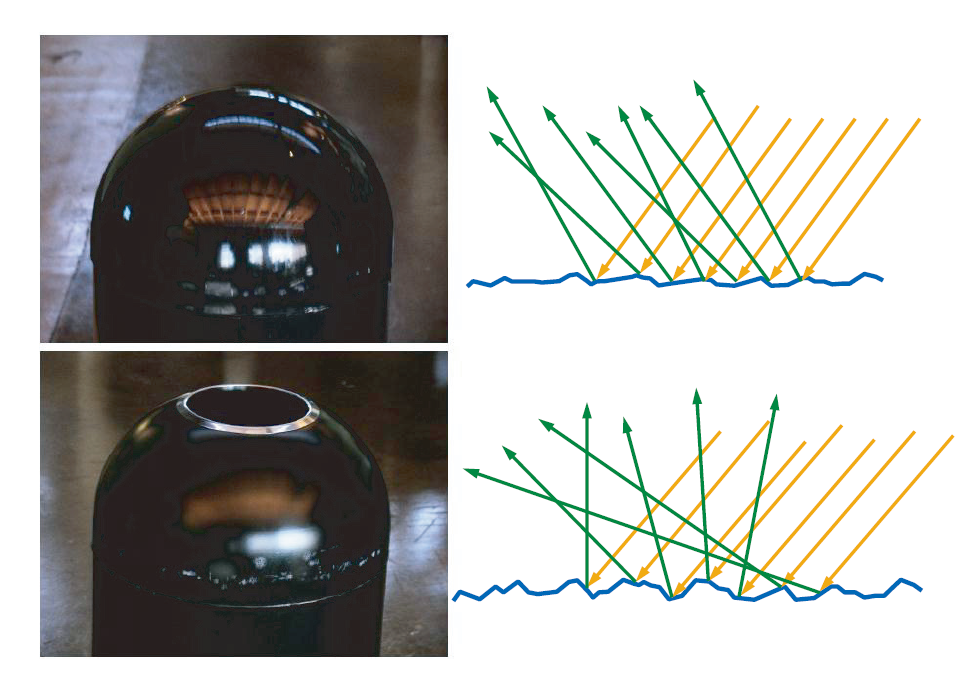
除了反射,还有折射的现象,它取决于被照射对象的本身:
- 对于金属,折射光会被吸收
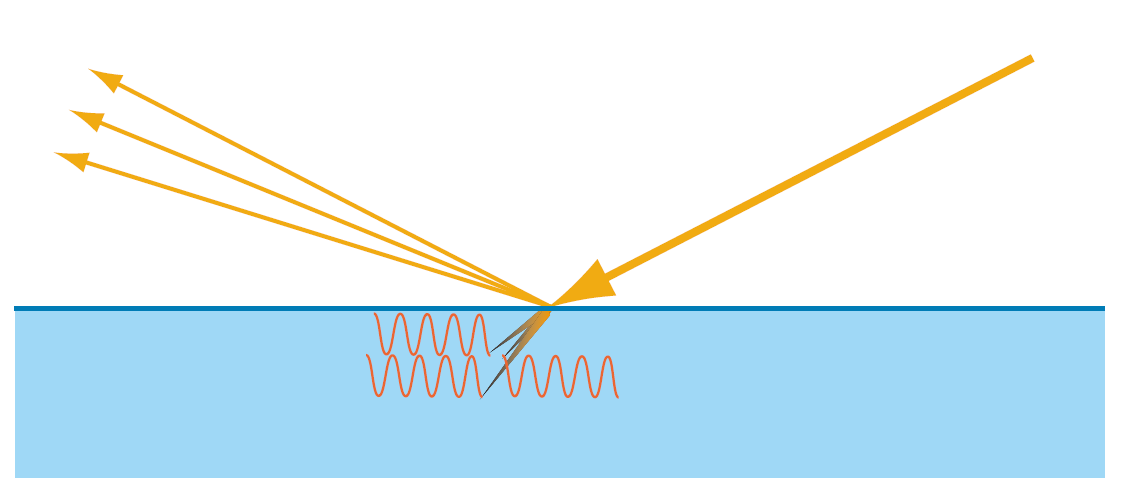
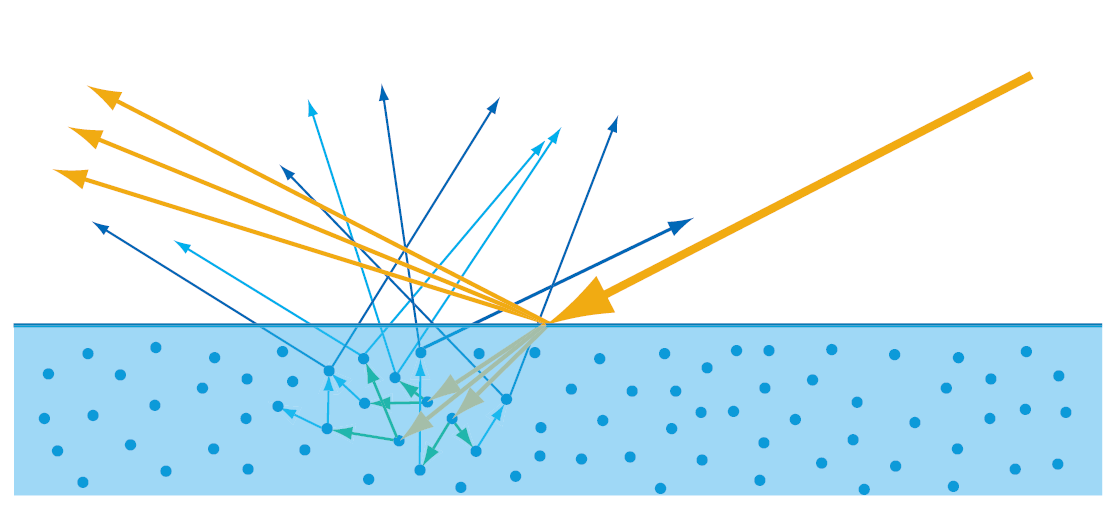
- 对于非金属,折射光会进行散射,有的会在物体内消耗殆尽,有的会从表面重新射出,重新射出的光也称次表面散射光(subsurface-scattered light),如果这些重新射出的光离入射点距离在一个像素内,则可以忽略,进行局部着色渲染,但是大于一个像素距离不能够忽略,则需要用一个特殊的渲染模型,即次表面散射渲染技术,下方暂不讨论该情况。
Cook-Torrance BRDF
对于微平面理论中的次表面散射也被认为是微观角度的漫反射,而Cook-Torrance BRDF就是考虑到上述镜面反射情况和漫反射情况的BRDF,定义如下:
$$ f_r=f_{lambert}+f_{cook-torrance} $$
$$ f_r=k_df_{diffuse}+k_sf_{specular} $$
其中$k_d$和$k_s$分别是漫反射项和镜面反射项分别占比,这两个相加等于1。
$f_{lambert}$ 和$f_{cook-torrance}$分别是漫反射和镜面反射的BRDF,接下来就这两个BRDF的推导。
漫反射项推导:
$f_{lambert}$它是相当于是将反射光均匀的分布在一个半球方向,所以我们可以推出它,如下图:

上图求出$\pi$的过程省略了,这里加上:
$$ \int^{2\pi}_0\int^{\frac \pi 2}_0 \cos\theta_i*\sin\theta_i d\theta_i d\phi_i=\pi $$
之前在《PBR理论基础1》里面算过$dwi$等于$\sin\theta d\theta d\phi$,这里对半圆所有向量积分,通过极坐标变式后,可得上式。
但是图中的式子还有一个问题就是没有考虑到能量的吸收,这里需要增加一个变量,注意这里的$\rho$是一个三维变量,表示漫反射光线的比重,也被常称为漫反射颜色。
$$ f_{diffuse}=\frac \rho \pi $$
镜面反射项:
首先看公式:
$$ f_{cook-torrance}=\frac {F(l,h)G(l,v)D(h)} {4(n*l)(n*v)} $$
这里的$l$是入射方向,$v$是反射方向,$n$为宏观法线向量,$h$为微平面法线向量。
比较重要的就是分子上的三个函数:
- $D(h)$是法线分布函数(Normal Distribution Function),描述微面元法线分布的概率,即正确朝向的法线的浓度。即具有正确朝向,能够将来自l的光反射到v的表面点的相对于表面面积的浓度。
- $G(l,v)$是几何分布函数(Geometry Function),描述微平面自成阴影的属性,即m =
· h的未被遮蔽的表面点的百分比。 - $F(l,h)$是菲涅尔方程(Fresnel Rquation),描述不同的表面角下表面所反射的光线所占的比率,也就是上文的$k_s$。
$D(h)$法线分布函数更直观的说,它的物理含义是法向量为h占微平面的面积,但是是在以下条件下的:
- 仅关注一个着色点,即单位面积。
- 每单位立体角。
(第二个条件是由于$h$是一个离散数值,而D函数是连续的,所以是不可能精确找到某个法线为固定值的微平面,可以类比为在概率论里面,连续型随机变量取一点的概率为0,再通俗一点就是无穷个数里面去某个数的概率为$\frac {1} {\infty}$,即为0)
所以D函数的真正物理意义是每单位面积,每单位立体角所有法向量为h的微平面的面积,那么h是怎么确定的呢?实际上在计算BRDF时,指定光方向$l$和视图方向$v$。这意味着所有表面点,只有那些恰好正确朝向可以将$l$反射到$v$的那些小平面可能有助于BRDF值(其他方向有正有负,积分之后,相互抵消),通过简单地推导可得知,$h$就是$l$和$v$的半矢量(half-vector)或半角矢量(half-angle vector),即$h=\frac {l+v}{|l+v|}$。
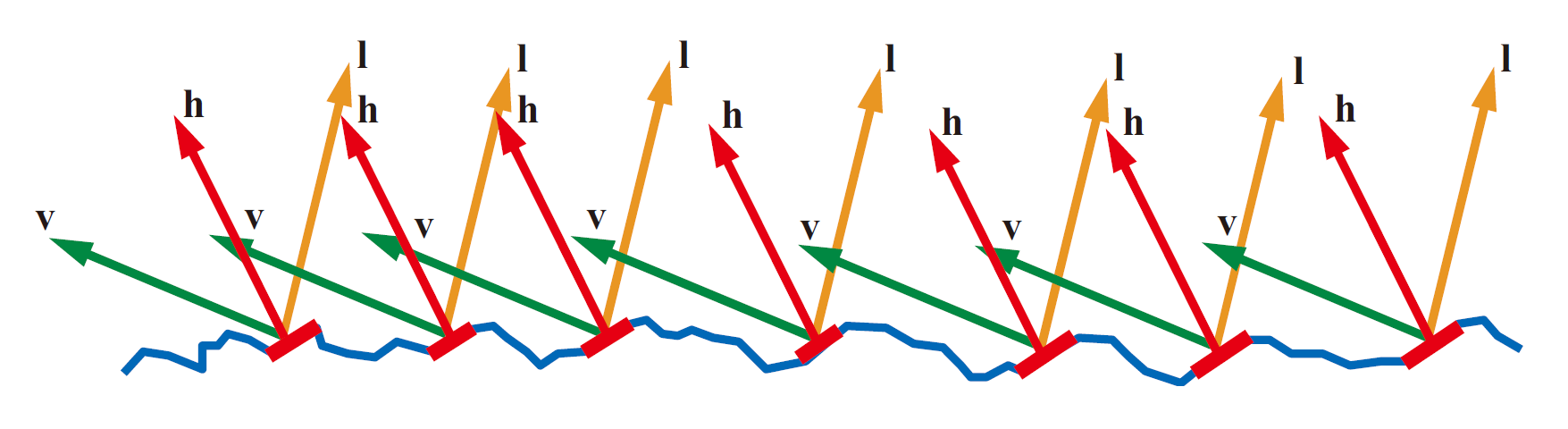
$G(l,v)$和$F(l,h)$都是描述光照的损失,1表示没有损失。
$G(l,v)$几何分布函数假设当一个平面很粗糙的话,它就会有可能遮挡其他微平面的反射的光线,在实际中被遮挡的光会进行多次表面散射,但是微平面理论中直接忽略了这些被遮挡的光。
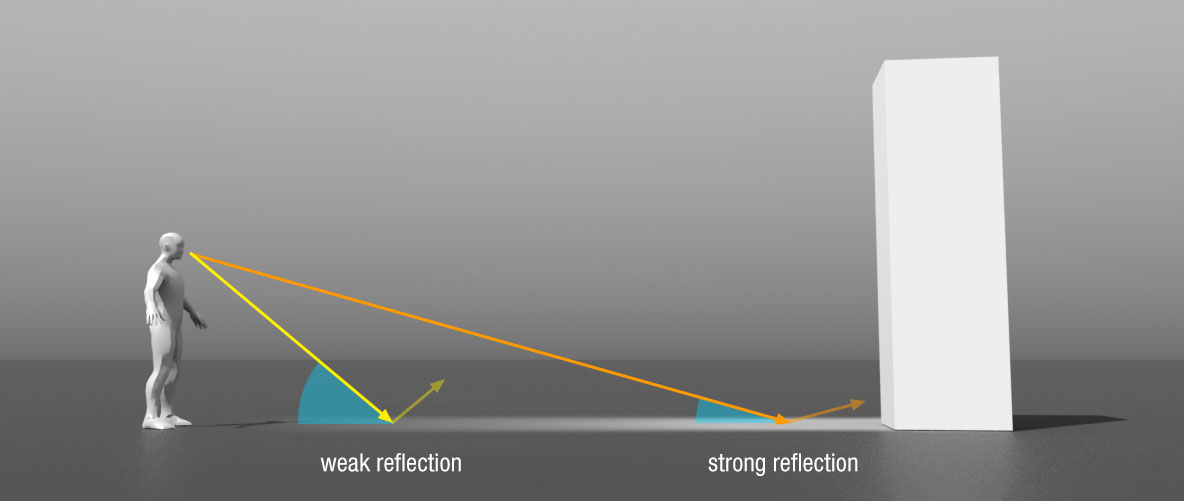
$F(l,h)$菲涅尔函数如果实现过RayTracing的电介质材质(玻璃材质),就会知道观察角度和平面法线的夹角较小,则呈折射特性,较大则呈反射特性。
分母部分$4(n*l)(n*v)$,校正因子(correctionfactor),作为微观几何的局部空间和整个宏观表面的局部空间之间变换的微平面量的校正,实际的推导过程在我参考的第二篇文章中,需要一定数学基础。
常见模型
D函数法线分布函数
法线分布函数(Normal Distribution Function, NDF)D的常见模型可以总结如下:
- Beckmann[1963]
- Blinn-Phong[1977](也就是《入门精要》中高光计算式,$D(h)=(n*h)^{gloss}$)
- GGX [2007] / Trowbridge-Reitz[1975]
- Generalized-Trowbridge-Reitz(GTR) [2012]
- Anisotropic Beckmann[2012]
- Anisotropic GGX [2015]
其中,业界较为主流的法线分布函数是GGX(Trowbridge-Reitz),因为具有更好的高光长尾:
$$ a=roughness^2 $$
$$ D_{GGX(m)}=\frac {\alpha^2}{\pi((n*m)^2(a^2-1)+1)^2} $$
F函数菲涅尔方程
菲涅尔项的常见模型可以总结如下:
- Cook-Torrance [1982]
- Schlick [1994]
- Gotanta [2014]
对于菲涅尔(Fresnel)项,业界方案一般都采用Schlick的Fresnel近似,因为计算成本低廉,而且精度足够:
$$ F_{Schlick}(v,h)=F_0+(1-F_0)(1-(v*h))^5 $$
$$ F_0=lerp(0.04,\rho,metalness) $$
其中$\rho$是物体表面颜色,一般由贴图采样决定。
G函数几何分布函数
几何项G的常见模型可以总结如下:
- Smith [1967]
- Cook-Torrance [1982]
- Neumann [1999]
- Kelemen [2001]
- Implicit [2013]
另外,Eric Heitz在[Heitz14]中展示了Smith几何阴影函数是正确且更准确的G项,并将其拓展为Smith联合遮蔽阴影函数(Smith Joint Masking-Shadowing Function),该函数具有四种形式:
- 分离遮蔽阴影型(Separable Masking and Shadowing)
- 高度相关掩蔽阴影型(Height-Correlated Masking and Shadowing)
- 方向相关掩蔽阴影型(Direction-Correlated Masking and Shadowing)
- 高度-方向相关掩蔽阴影型(Height-Direction-Correlated Masking and Shadowing)
目前较为常用的是其中最为简单的形式,分离遮蔽阴影(Separable Masking and Shadowing Function)。
该形式将几何项G分为两个独立的部分:光线方向(light)和视线方向(view),并对两者用相同的分布函数来描述。根据这种思想,结合法线分布函数(NDF)与Smith几何阴影函数,于是有了以下新的Smith几何项:
- Smith-GGX
- Smith-Beckmann
- Smith-Schlick
- Schlick-Beckmann
- Schlick-GGX
其中UE4的方案是上面列举中的“Schlick-GGX”,即基于Schlick近似,将k映射为k=a/2,去匹配GGX Smith方程:
$$ k=\frac a 2, a=(\frac {roughness+1}{2})^2, G_1(v)=\frac {n*v}{n*v*(1-k)+k}, G(l,v,h)=G_1(l)G_1(v) $$
这里公式还有一种表示方式,感觉是更加偏向实际运用的,这里也列出来:
$$ k_{direct}=\frac{(roughness+1)^2}{8}, k_{IBL}=\frac {roughness^2}{2}, G_{sub}(n,v,k)=\frac {n*v}{(n*v)*(1-k)+k}, G(n,v,l,k)=G_{sub}(n,v,k)*G_{sub}(n,l,k) $$